A Hohmann transfer calculation changes the circular orbit of a spacecraft using an impulse burn along the prograde direction of the initial orbit. Real spacecraft burns take time, e.g. the Apollo transfer to the moon requires a burn of about 350 seconds. I was recently asked by a developer using Gravity Engine about how the spacecraft should steer during this burn time. Should it keep the initial attitude when the burn started? Burn “forward”? Burn perpendicular to the Earth radius vector? Great question! (The question comes from the developer of ReEntry, a must have if you’re a vintage space buff!)

In the interests of not re-inventing the wheel and limiting the amount of “rocket science” I do, l first turned to my bookshelf, Google and the literature. Unsurprisingly, this is a “whole thing”. Since the trajectories of missions are planned using highly detailed iterative simulations coupled with optimal control theory the literature is highly technical and not something I can easily map into Gravity Engine. Instead I decided I would do some basic experiments with three steering laws:

1. Lock on to the initial burn direction and maintain it.
2. Burn in the “forward” direction
3. Burn perpendicular to the Earth orbit radius in the orbital plane

In addition to direction, there is an issue of timing. If the burn will be on the order of 350 seconds, where should the burn start with respect to the desired destination point? Instead of varying this as an input parameter, I elected to measure the result when arriving at the destination: how far away from the point opposite where the burn started did the ship reach the destination orbit?

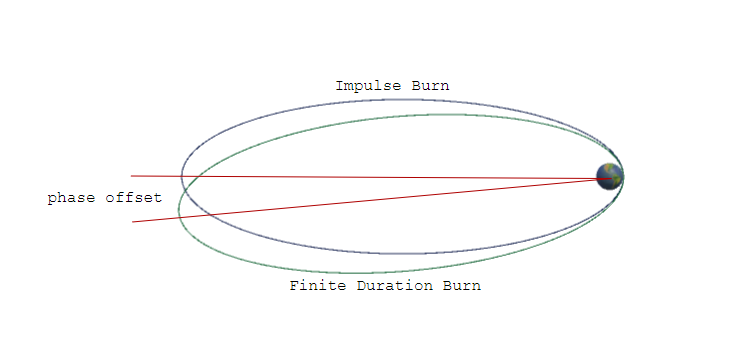
It’s always fun to think about the physics here and try and guess which steering mode will give the most efficient transfer. My guess was that by thrusting perpendicular the maximum amount of angular momentum would be added and this approach would use the least fuel. I then build a scene in Gravity Engine to assess these choices.

Gravity Engine allows a direct Hohmann transfer to be computed via its TransferShip component. This is used to provide a reference transfer. Since the scenario I was asked about was related to Apollo, I used some approximate values for ship, stage and fuel mass and used a rocket engine model that accounted for the decrease in mass as the ship burned fuel. I then created a FiniteBurn component to run the steering algorithm. I have archived this demonstration code for interested users of GE.

The results are:

		Mode	Actual Burn Time	Phase Offset
SIVB Engine		Tangent	299.6	11.03
		Perpendicular	299.79	12.52
		Fixed	303	4.79

Three things about this are interesting:

1. The total burn time to reach an apogee at the Moon’s distance is not very strongly affected by the choice of steering law.
2. The angle offset of the arrival point is strongly affected by the choice. The timing of when to start the burn DOES depend strongly on the steering law.

It’s a good thing I do experiments instead of trusting my intuition. Thrusting perpendicular to the radius was not the most efficient steering law.