Earth to Moon: Free Return With Patched Conics

Planning a trajectory to the moon is tricky. The motion of the ship in the combined gravitational field of the earth and the moon brings us to the “full-on” three body problem in orbital dynamics. This means that there are no elegant solutions in terms of basic mathematical functions and small changes in initial conditions can have large effects in the evolution of the trajectory. This is especially true in the earth-moon system in particular since the moon is both relatively heavy compared to the earth, and reasonably close to the earth. The normal way forward is to develop a model of the system and then do numerical 3 or 4 body (adding the sun) trial and error experiments using algorithms to try variations in initial conditions and determine if the resulting trajectory gets to the desired point around the moon.

A good starting point to develop intuition and guide initial condition selection is to use a simplified model in which the ship evolves in the earth’s gravity until it is within the moons “sphere of influence” and then model the path purely in the moon’s gravity. Each trajectory will be a conic (ellipse or hyperbola) and the approach is named the “patched conic” approach. This approach was used as a starting point for the Apollo missions, although it is not reliable enough to “fly by” it does help guide the choice of starting conditions. In Gravity Engine, we can choose to evolve the spaceship in Kepler mode (“on-rails”) and hence can actually match the path planned with patched conics very closely. For many games, this will be a good model of transit to the moon.

GE provides a series of scenes in the Minigames/FreeReturn folder that determine a path to the moon and the resulting return to earth if the moon insertion burn is skipped. They allow a target perilune to be specified and allow the user to interactively tune the burn parameters to achieve a specific perigee in the earth return orbit.

Even with the patched conic simplification there are a handful of parameters that need to be explained to provide an understanding of the way to plan a trajectory to the moon and a free return.

One classic reference for this material (used in the development of this code) is Fundamentals of Astrophysics. It has clear presentation and, as is typical of Dover books, is very affordable. A recent reference is the paper Optimal Round Trip Lunar Missions based on the Patched Conic Approximation.

The starting scenario is that the ship is in a circular parking orbit around earth and that this orbit is co-planar with the moon. The moon orbit is also assumed to be circular. The patched conic initial conditions are show in Figure 1.

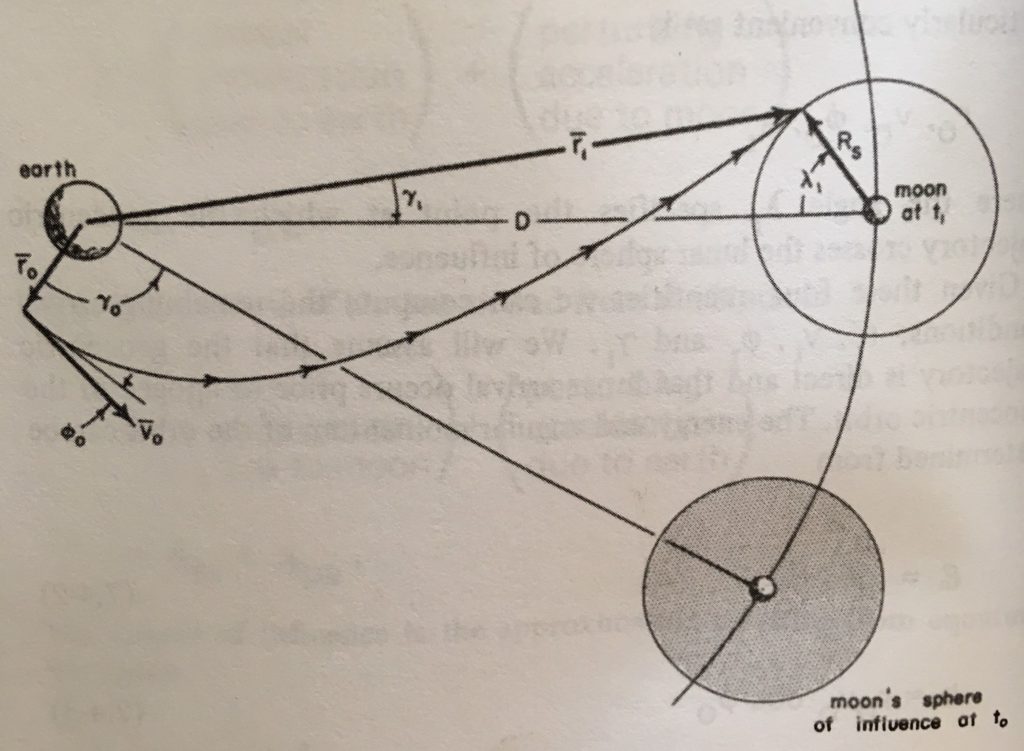
Figure 1: Reference diagram for TEI burn. From Fundamentals of Astrophysics (https://store.doverpublications.com/0486497046.html)

The inputs to the calculations are:

  • r0: the radius of the ship parking orbit around earth
  • v0: the magnitude of the velocity of the departure burn
  • \phi_0 / phi0: the “flight path angle” or deviation from the local horizon of the direction of the burn. This is typically zero or some small value.
  • \lambda_1 / lambda1: the angle from the earth-moon line at the time of SOI entry to the point on the SOI where the ship enters the moon’s gravity

By specifying r0 and lambda1 the end points of a conic have been established, however there are many conics that could fit between these points. The parameters v0 and $\phi_0$ specify a velocity vector at r0 and therefore determine a specific conic (usually a departure ellipse). Given this departure path the next steps in the algorithm determine the velocity with respect to the earth at SOI entry (r1, v1) and then determine the position and velocity with respect to the moon (r2, v2). The variable (r2,v2) fully determine an orbit around the moon and this allows the resulting perilune to be determined. Following the path out the the SOI then establishes an SOI exit point and the transforming back to the earth sphere gives an earth orbit and the free return perigee. [There is a slight tweak needed here, since as the ship is moving around the moon, the moon is moving around the earth and this needs to be taken into account].

Free Return GE Scripts

To operationalize this algorithm several scripts are provided for the free-return mini-games. They are summarized below and then described in more detail.

  • ComputeTLIController: Main controller in the scene and the place where the target perilune is specified. Accepts keyboard input to adjust values of lambda_1 and phi_0 and updates orbit predictors and graph to show the resulting trajectories.
  • ComputeTLI: A stand alone script that determines the perilune achieved from a specific set of (r0, v0, lambda1, phi0)
  • PerformTLI: On user input, converts the current trajectory preview into maneuvers and adds them to the GE maneuver queue
  • FreeReturnCorrection: Once the TLI burn has happened this script can compute the delta required to ensure the correct perilune is achieved.

The general user usage is:

  1. Set the initial estimates for lambda0 and phi0 in the inspector for ComputeTLIController.
  2. Start the scene.
  3. Adjust values using IKOL for lambda1 and WS for phi1 and R (to select first or second root) until the desired free return perigee is displayed.
  4. Use ‘X’ to execute the maneuver.
  5. Use time zoom (1-8) to speed things up.
  6. Use F2 to move the camera to follow the ship, and watch the trajectory evolve.

Outline of Script Operation

ComputeTLI

The role of ComputeTLI is to determine the perilune for a specific choice of (r0, v0, lambda1, phi0) by using the algorithm from Fundamentals of Astrodynamics.

The outputs of this script are:

  • perilune
  • \gamma_0: the angle from the earth-moon line at the time of the TEI burn to the orbit position where the burn must take place (see Figure 1)

This script is called repeatedly from the ComputeTLIController to evaluate a range of potential v0 values.

ComputeTLIController

The controller manages the values of the initial conditions for the burn (lambda1, phi0) and finds the perilune value for a range of v0 values based on the minimum v0 required to leave the earth and reach the moons altitude. It then walks the resulting value table to find the velocity for which the target perilune is achieved. To help the user visualize this process the script plots the results of this search in a plot window using a PlanningPlot component, a light-weight line plotter developed for this role.

The controller interpolates a v0 to achieve the requested perilune and then uses values from the ComputeTLI component to determine the required velocities at SOI entry to program OrbitPredictors to illustrate the trajectory that will be achieved. These orbits are shown with respect to the existing moon position, even though in reality they would be rotated to correspond to the actual moon position for that segment of the flight.

PerformTLI

The execution of the transfer is handled by PerformTLI. This script has a reference to the ComputeTLIController and retrieves the required v0, phi0 and gamma0 for the transfer. It performs the following operations:

  1. Determines the time required for the ship to rotate around to the correct angle with respect to the current moon position (accounting for the fact that the moon is also moving as the ship orbits into position).
  2. Creates a maneuver for TLI using the values of v0 and phi0 from the controller.
  3. If the ship is in Kepler mode, adds a maneuver at the time of SOI entry to change the ship the moon’s sphere of influence.
  4. During the SOI entry maneuver, determines another maneuver for SOI exit to move the ship back to the earth’s sphere of influence.

FreeReturnCorrection

In Kepler mode the maneuvers created typically result in a perilune that is close to the target perilune. Once the maneuver has been executed it can be further improved during the transit to the moon by the script. Pressing M will adjust the ship velocity to achieve the target TLI.

The adjustment is determined by using OrbitPropagators to evolve the ship to the SOI and then to determine the perilune one the orbit has been continued in the moon’s gravity. A root finder is used to find an adjustment to the ships current velocity magnitude to achieve the desired perilune.

Return to Earth (TEI)

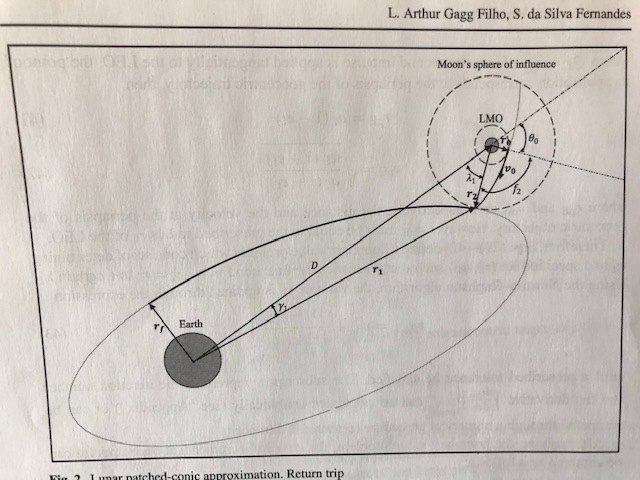
The patched conic return to earth is demonstrated in the scene PatchedConicTEI_XZ. The scene assumes that the ship is in a circular lunar orbit in the same plane as the moon’s orbit around the earth. The inputs to the determination of the TEI burn are:

  • r1: the radius of the ship’s orbit (taken from the ship NBody)
  • \lambda_1 / lambda1: the angle of the point of SOI exit to the earth moon line
  • phi_1 / phi1: the flight path angle of the burn (angle of the burn direction to the local horizontal of the ship orbit)

Given these parameters the position and velocity at SOI exit can be determines and then continued into the earth’s sphere of influence. This allows the perigee of the earth orbit to be determined. The calculation also determines the point in the ship orbit where the burn needs to take place, theta0.

Reference for return to Earth parameters. From Optimal round trip lunar missions based on the patched conic approximation. (Filho and Fernandes, 2015).

TEI Scripts

The scripts here use the same structure as in the TEI scene above. The scripts are:

  • ComputeTEI: Performs the core calculation of perigee for a given set of input parameters.
  • ComputeTEIController: Main controller for the scene. Using ComputeTEI it evaluates a series of possible velocity changes and plots the resulting perigee. It then selects a velocity that achieves the target perigee. User input to adjust lambda1 and phi1 is handled.
  • PerformTEI: Map the trajectory determined by the ComputeTEIController into maneuvers to be executed by the ship in the scene.
  • ReturnCourseCorrection: Once the ship has entered the earth’s SOI this script will adjust the perigee to the target perigee without altering any other orbital parameters.