The FRGeneric scene demonstrates the path a ship will take from Earth orbit to a Moon flyby and the resulting final orbit around the Earth. It allows a user to alter the time of flight and the arrival angle at the Moon’s sphere of influence and shows the resulting circumlunar trajectory and orbit around Earth. The goal is to find a path that approaches the Moon at a required distance and returns to the Earth’s atmosphere. This way if the ship is unable to fire an engine to enter lunar orbit it will return safely to Earth.

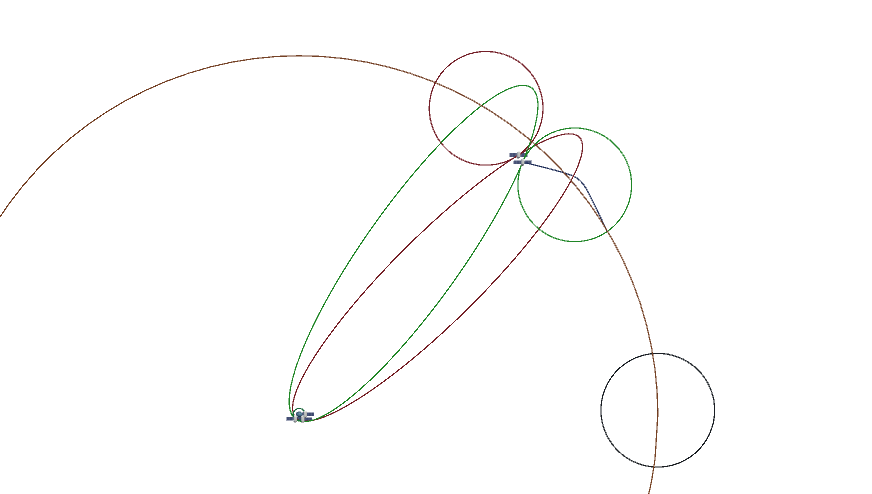
The orbital mechanics for this scenario involves the dreaded three-body problem (Earth, Moon, Spaceship). There are no closed form solutions for this problem and the only way to obtain a fully accurate solution is to simulate the path for each set of initial conditions. The FRGeneric scene makes use of a patched conic approximation that treats the problem as a series of two-body problems: Earth to Moon SOI, around Moon and Moon SOI to Earth. Each of this segments is interactively updated as the user changes the inputs of time to SOI and SOI arrival angle. (Work has started on a full N-Body version with iterating N-body trajectories)

The implementation of this scene makes use of a number of interesting and valuable features of the OrbitUniversal class as well as the LambertBattin class. This documentation page will provide some details on its implementation.

Earth to Moon: Positioning the Moon

The first conic patch is the orbit from the Earth to the Moon, given a time of flight (TOF) and SOI arrival point. The first thing that needs to be determined is where the Moon will be after the specified TOF. The FRGeneric scene allows the Moon to be in an arbitrary elliptical orbit and the the FRGenericController has some code to determine this as the first part of the ComputeTransfer() method.

Prior to calling the ComputeTransfer method, the controller creates two clones of the Moon. One to show the Moon at the point of SOI entry and a second to show the position when the spacecraft leaves the SOI. These “ghost moons” have the same orbital properties as the original moon and are used to find the future position of the Moon given the user-specified time of flight.

The code to create the ghost moons is:

for (int i = 0; i < 2; i++) {
   GameObject ghostMoonGO = Instantiate(moonBody.gameObject);
   ghostMoon[i] = ghostMoonGO.GetComponent<NBody>();
   ghostMoonOrbit[i] = ghostMoonGO.GetComponent<OrbitUniversal>();
}
ghostMoon[MOON_SOI_ENTER].gameObject.name = "GhostMoon (SOI enter)";
ghostMoon[MOON_SOI_EXIT].gameObject.name = "GhostMoon (SOI exit)";

ghostMoon[MOON_SOI_ENTER].GetComponentInChildren<LineRenderer>().material =   toMoonMaterial;
ghostMoon[MOON_SOI_EXIT].GetComponentInChildren<LineRenderer>().material = fromMoonMaterial;

This code clones the entire Moon object in the scene, including the object that draws the SOI. To distinguish the SOI for the arrival and departure ghost moons a material is assigned for each in some code after their creation.

Specifying the time of flight as an absolute number would be difficult since it depends on the mass of the Earth and the initial orbit and the user may not have a good intuition for these values. The FRGeneric scene instead uses a relative time: the percentage of the Hohmann transfer time required to reach the Moon’s orbit (assuming the Moon’s orbit is circular). This is the purpose of the variable tFlightFactor set in the inspector. Given the time of flight the next task is to position the Moon at this future time. This will also define the position of the first maneuver which will happen on the Earth-Moon line on the opposite side of the Earth from the Moon.

The code to position the Moon is:

double timeNow = ge.GetPhysicalTimeDouble();
// First using the transfer time, move the ghost Moon to position at SOI arrival. 
// Call evolve via LockAtTime on the ghostMoon to move it. Set position based on this.
double t_flight = tflightFactor * timeHohmann;
double timeatSoi = timeNow + t_flight;
ghostMoonOrbit[MOON_SOI_ENTER].LockAtTime(timeatSoi);

The key line to set the moon at the correct location for SOI arrival is the use of the LockAtTime() method. This calls evolve on the Moon orbit at the specified time and locks the result (this ensures calls to determine the position at the current time by GE will be skipped). This method is only available if the moon is set to evolve in KEPLER_MODE (i.e. is on rails). It results in a call to the Kepler evolution code and updates the internal position and velocity and GE will use these values when updating NBody objects as part of its evolve loop.

Earth to Moon: Using “Ghost Ships”

The next step is to determine the transfer to a point on the Moon’s SOI. This is done by using a Lambert transfer. This transfer determines the initial and final velocities given a start and end point and transit time. The first task is to determine the SOI arrival point. This is accomplished by the use of “Ghost ships”. These are additional copies of the spaceship placed at the start and end points of each of the patched conic segments. Their creation is similar in concept to the creation of the ghost moons with some additional details to configure the orbit predictors and orbit universal center objects for each case. The details can be seen in the AddGhostBodies() method in the FreeReturnGeneric controller.

The first step is to determine the ship start position. The ship will perform its TLI maneuver at a point referenced with respect to the Earth-Moon line on the side of the Earth opposite the moon. The user parameter shipTLIAngleDeg controls how far away from the Earth-Moon line the departure point will be. This is programmed into the TLI ghost ship orbit phase to determine the correct departure point. The code to do this is:

    // Place the TLI ship at the user-requested angle wrt planet-moon line
    // Put ghost ship in same orbit geometry as the moon, assuming it is circular. Then 
    // can use same phase value. 
    // (Ship needs to reach this departure point, it may not even be on the ship orbit
    //  in general). 
    ghostShipOrbit[TLI].phase = shipTLIAngleDeg + (moonPhase + 180f);
    ghostShipOrbit[TLI].inclination = ghostMoonOrbit[MOON_SOI_ENTER].inclination;
    ghostShipOrbit[TLI].omega_lc = ghostMoonOrbit[MOON_SOI_ENTER].omega_lc;
    ghostShipOrbit[TLI].omega_uc = ghostMoonOrbit[MOON_SOI_ENTER].omega_uc;
    ghostShipOrbit[TLI].p_inspector = shipOrbit.p;
    ghostShipOrbit[TLI].Init();
    ghostShipOrbit[TLI].LockAtTime(0);

Next the code needs to determine the end point. The ENTER_SOI ghost ship has an OrbitUniversal component with a size equal to the SOI radius. The remaining orbital elements are copied from the moon to ensure the arrival point at the SOI is in the same plane as the moon’s orbit around the planet.

// Place the SOI enter ship at the user-requested angle in an SOI orbit. Lock at time 0 so the phase     
// is held per the user input.      
ghostShipOrbit[ENTER_SOI].phase = soiAngleDeg + moonPhase;     ghostShipOrbit[ENTER_SOI].inclination = soiInclination + shipOrbit.inclination;     ghostShipOrbit[ENTER_SOI].omega_lc = ghostMoonOrbit[MOON_SOI_ENTER].omega_lc;     ghostShipOrbit[ENTER_SOI].omega_uc = ghostMoonOrbit[MOON_SOI_ENTER].omega_uc;     ghostShipOrbit[ENTER_SOI].Init();     ghostShipOrbit[ENTER_SOI].LockAtTime(0);

Now that both end points for the path to the SOI entry point have been determined the required velocities at the start and end points can be determined by using the LambertBattin transfer. This is done via:

// Use Lambert to find the departure velocity to get from departure to soiEntry     
// Since we need 180 degrees from departure to arrival, use LambertBattin     
lambertB = new LambertBattin(ghostShip[TO_MOON], planet, departurePoint, soiEntryPos, shipOrbit.GetAxis());

As the comment indicates, LambertBattin is used instead of LambertUniversal. LambertUniversal does not allow a transfer from A to B when A and B are on opposite sides of the planet (180 degrees apart). LambertBattin handles this case.

Then the first segment of the orbit can be initialized using the position, velocity and time. The final velocity and position are used to determine the hyperbolic orbit around the moon. In both cases this is done by initializing the OrbitUniversal for each segment with the InitFromRVT() method.

    ghostShipOrbit[TO_MOON].InitFromRVT(departurePoint, lambertB.GetTransferVelocity(), timeNow, planet, false);     // Set velocity for orbit around moon. Will be updated every frame     ghostShipOrbit[SOI_HYPER].InitFromRVT(soiEntryPos, lambertB.GetFinalVelocity(), timeNow, ghostMoon[MOON_SOI_ENTER], false);

Around the Moon

The SOI_HYPER ghost ship now has the correct orbit around the moon. Now a ghost ship needs to positioned at the SOI exit point to determine the orbit around the Earth after the ship eaves the moon gravitational influence. The first step is to determine the time that will be required to swing around the moon. This time will determine the moon position at SOI exit and the second ghost moon can be moved to this position.

First the code to find the SOI exit position relative to the moon:

    // Find the exit point of the hyperbola in the SOI
    OrbitUtils.OrbitElements oe = OrbitUtils.RVtoCOE(soiEntryPos, lambertU.GetFinalVelocityDouble(), ghostMoon[MOON_SOI_ENTER], false);
    Vector3d soiExitR = new Vector3d();
    Vector3d soiExitV = new Vector3d();
    OrbitUtils.COEtoRVMirror(oe, ghostMoon[MOON_SOI_ENTER], ref soiExitR, ref soiExitV, false);

    // Find time to go around the moon. TOF requires relative positions!!
    Vector3d ghostSoiEnterPos = ge.GetPositionDoubleV3(ghostMoon[MOON_SOI_ENTER]);
    Vector3d soiEnterRelative = soiEntryPos - ghostSoiEnterPos;
    Vector3d soiExitRelative = soiExitR - ghostSoiEnterPos;
    Vector3d soiExitVelRelative = soiExitV - ge.GetVelocityDoubleV3(ghostMoon[MOON_SOI_ENTER]);
    double hyperTOF = ghostShipOrbit[SOI_HYPER].TimeOfFlight(soiEnterRelative, soiExitRelative);

This code uses the OrbitUtils method COEtoRVMirror. This takes the COE (Classical Orbital Elements) and a position and finds the mirror position on the other side of the orbit. This is then used to find a relative position that can be used in the OrbitUniversal TimeOfFlight() method. The result is the time to pass through the Moon’s SOI. This can then be used to position the second ghost moon via:

    // Position the ghost moon for SOI exit (timeAtSoi includes timeNow)
    t_soiExit = timeatSoi + hyperTOF;
    ghostMoonOrbit[MOON_SOI_EXIT].LockAtTime(t_soiExit);

Finally the ghost ship for SOI exit can be put in the correct position and given the exit velocity determined by using the hyperbola mirror method:

    // Set position and vel for exit ship, so exit orbit predictor can run. 
    Vector3d ghostMoonSoiExitPos = ge.GetPositionDoubleV3(ghostMoon[MOON_SOI_EXIT]);
    Vector3d ghostMoonSoiExitVel = ge.GetVelocityDoubleV3(ghostMoon[MOON_SOI_EXIT]);

    ghostShipOrbit[EXIT_SOI].InitFromRVT(soiExitRelative + ghostMoonSoiExitPos, 
                                         soiExitVelRelative + ghostMoonSoiExitVel, 
                                         timeNow, planet, false);

All three conic segments have now been determined and displayed. When the user choses to execute the transfer the orbital and time information determined in ComputeTranfer() is used to build a KeplerSequence from the information held by the ghost ships. This is done by collecting the RVT information from each ghost ship and using these in the OrbitUniversal segments in the KeplerSequence.

private void TransferOnRails() {
    // the ship needs to have a KeplerSequence
    KeplerSequence kseq = spaceship.GetComponent();
    if (kseq == null) {
        Debug.LogError("Could not find a KeplerSequence on " + spaceship.name);
        return;
    }
    // Ellipse 1: shipPos/shipvel already phased by the caller.
    double t_start = ge.GetPhysicalTime();
    double t_toSoi = timeHohmann * tflightFactor;
    KeplerSequence.ElementStarted noCallback = null;
    Vector3d r0 = new Vector3d();
    Vector3d v0 = new Vector3d();
    double time0 = 0;
    ghostShipOrbit[TLI_TO_MOON].GetRVT(ref r0, ref v0, ref time0);
    kseq.AppendElementRVT(r0, v0, t_start, true, spaceship, planet, noCallback);

    // Hyperbola: start at t + transferTime
    // Need to add wrt to ghostMoon (relative=true), then for actual Kepler motion want it around moon
    ghostShipOrbit[SOI_HYPER].GetRVT(ref r0, ref v0, ref time0);
    OrbitUniversal hyperObit = kseq.AppendElementRVT(r0, v0, t_start + t_toSoi, true, spaceship, ghostMoon[MOON_SOI_ENTER], EnterMoonSoi);
    hyperObit.centerNbody = moonBody;

    // Ellipse 2: 
    ghostShipOrbit[EXIT_SOI].GetRVT(ref r0, ref v0, ref time0);
    kseq.AppendElementRVT(r0, v0, t_soiExit, true, spaceship, planet, ExitMoonSoi);
}

Now the ship will follow the three conic patches around the moon, following the path that was determined by the user’s time of flight and SOI entry specifications.