Lunar Transfer/Lunar Course Correction

A transfer from a planet to a moon with significant gravity requires an approach that considers the effect of the moons gravitation. One of the more challenging scenarios is a transfer from the Earth to the Moon, since the Moon is a significant fraction of the Earths mass. It is the most complex lunar transfer in the solar system.

In practice, to get a highly accurate transfer an N-body simulation is run with the specific mission constraints and the transfer velocity and transfer time is found by repeating these simulations varying the initial conditions until a suitable solution is found. The solution is very sensitive to small changes in the velocity and time, so it is expected that course corrections will be required during the transfer.

The starting point for these simulations is a calculation using patched conics to determine an approximate time and velocity for the transfer.

Gravity Engine provides a class to perform this patched conic calculation and a simple course correction mechanism that can be used while in-transit. These scripts can be seen in action in the scenes:

Scenes/Demos/MiniGames/EarthMoonXfer: Shows Earth/Moon system in ORBITAL units
Scenes/Demos/MiniGames/MoonXfer: Shows a transfer in DIMENSIONLESS units with a shorter transfer time.

Both scenes make use of the GEConsole. This provides a simple way to trigger the commands and to see the code required to determine the transfer and course correction.

Patched Conic Transfer

A patched conic transfer is computed by the class PatchedConicXfer. A typical invocation (taken from the OrbitMGController in the MoonXfer scene) is:

 OrbitTransfer xfer = new PatchedConicXfer(shipOrbit, moonOrbit, lambda1);

The constructor declarations is:

 public PatchedConicXfer(OrbitData fromOrbit, OrbitData toOrbit, float lambda1Deg) : 
 base(fromOrbit, toOrbit)

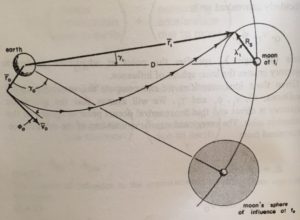
In the construction of a PatchedConicXfer the arguments require the orbit of the ship and the orbit of the moon as well as a parameter that indicates the targeted angle of arrival at the lunar sphere of influence. To be consistent with the technical literature, this parameter is labeled lambda1 (see image below).

This class extends the OrbitTransfer base class. This allows it to inherit the common code to maintain a list of maneuvers that execute the transfer. These can be added to GE via:

foreach (Maneuver m in xfer.GetManeuvers()) {
      GravityEngine.Instance().AddManeuver(m);
}

The code may optionally choose to add a callback to some maneuvers prior to adding them to GE.

The computation of the patched conic transfer follows the development in “Fundamentals of Astrophysics” by Bate, Mueller and While (1971, Dover Press). The illustration below shows the role that lambda1 plays in the computation.

In the general patched conic transfer, the spaceship initial position in the planetary orbit can be specified. To simplify the usage of the orbit transfer function, the implementation of PatchedConicXfer uses a Hohmann transfer to the moon, with correct phasing to determine the transfer point. It then makes use of the specified lambda1 value to determine the transfer velocity required. This result is then available as the OrbitTransfer maneuver.

The patched conic computation determines the maneuver required to arrive at a specific angle at the sphere of influence but does not constrain how close the spaceship will come to the moon as it continues into the lunar gravitational field. The best way to determine this approach distance is to run a simulation and find the point of closest approach. This is done by the LunarCourseCorrection class.

Lunar Course Correction

The LunarCourseCorrection class plays two roles in Lunar orbit transfer calculation:

Determine the future evolution of a maneuver and find the closest approach to the moon. This can be done either directly (incurring a frame rate hit) or asynchronously on a new thread with a callback.
Run three evolution simulations with a small change in the velocity of the spaceship and use these results to determine a course correction via linear interpolation. This mode runs each simulation on a new thread and can only be run asynchronously.

Both of these modes of operation are provided by the console commands available in the OrbitMGController class used in the MoonXfer and EarthMoonXfer scenes in Demos/Minigames/. This scene makes use of the GEConsole prefab and the game controller registers some orbit transfer commands with the console:

pcp <angle> : Compute the patched conic transfer and then run a ClosestApproach calculation (waiting for the result). Report and record the closest approach that results.
moonxfer/m <angle> : perform the moon transfer using patched conic transfer
lunar_correction/c: determine a course correction for the ship. This can only be run once the ship is on the way to the moon, and requires a previous pcp command (from which the target approach distance was saved internally)

To see these routines in operation the following video is taken from the PlanetMoonXfer minigame. A transcript of the key commands is provided below.

Demo Video

The sequence of key strokes to reproduce is:

Press backquote twice (to open, then enlarge the GEConsole)
Press ‘p’ to pause
‘pcp 75’ to see a preview of the lunar xfer
‘m 75’ to perform the transfer
‘go’ to restart (can optionally add ‘z 10’ to speed things up)
‘p’ to pause once transfer has happened
‘ap’ to execute approach prediction
‘c’ to do an asynchronous computation of the course correction to refine the target approach.

To understand how to use the LunarCourseCorrection class the code that implements these GEConsole commands provides a helpful reference. This code can be found at the bottom of the class controlling the scene: OrbitMGController. Excerpts of the code are provided here with some explanation.

Patched Conic/Course Prediction Code

 public string MoonPreview(string moonName, float lambda1) {
        // Step 1: Determine the patched conic xfer
        OrbitData shipOrbit = new OrbitData();
        NBody shipNbody = spaceshipCtrl.GetNBody();
        shipOrbit.SetOrbit( shipNbody, centralMass);
        OrbitData moonOrbit = new OrbitData();
        NBody moonNbody = GetTargetByName(moonName);
        moonOrbit.SetOrbit(moonNbody, centralMass);
        OrbitTransfer xfer = new PatchedConicXfer(shipOrbit, moonOrbit, lambda1);

        // Step 2: Make a copy of the universe state and evolve forward to find min distance to 
        // moon. 
        GravityEngine ge = GravityEngine.Instance();
        GravityState gs = ge.GetGravityStateCopy();
        // there is only one maneuver to add
        gs.maneuverMgr.Add(xfer.GetManeuvers()[0]);
        // run a simulation and find the closest approach (Expensive!)
        LunarCourseCorrection lcc = new LunarCourseCorrection(shipNbody, moonNbody);
        // want to be within 10% of Earth-Moon distance
        LunarCourseCorrection.CorrectionData data = new LunarCourseCorrection.CorrectionData();
        data.gs = gs;
        data.approachDistance = 0.1f * moonOrbit.a; ;
        data.correction = 0;
        data.maxTime = TIME_TO_MOON;
        // Direct (unthreaded) calculation
        predictedDistance = lcc.ClosestApproach(data);

        return string.Format("Patched Conic with lambda={0} => approach={1}\n", lambda1, predictedDistance);
    }

The first step is to use PatchedConicXfer() to determine the maneuver to transfer to the moon for the given lambda1. The code preceeding this call creates the OrbitData inputs using the objects in the scene.

The second step is the setup of a “what if” computation to determine the closest approach with the maneuver determined by PatchedConicXfer(). The ClosestApproach() computation requires a set of parameters in a CorrectionData struct. The fields in this struct provide input arguments and hold results about the closest approach once the computation is complete.

   public class CorrectionData {
        // args
        //! Gravity state to evolve [input]
        public GravityState gs;
        //! Closest approach checking only starts once objects are this close [input]
        public float approachDistance;
        //! time limit (in physics time) for evolution [input]
        public float maxTime;
        //! factor applied to spaceship velocity at start of calculation [input]
        public double correction;
        // results
        //! run-time used by the calculation in ms [output]
        public long execTimeMs;
        //! physics time at point of closest approach [output]
        public double timeAtApproach;
        //! distance in physics units at closest approach [output]
        public double distance;

        //! Clear the results
        public void Reset() {
            execTimeMs = 0;
            timeAtApproach = -1;
            distance = -1;
        }

    };

The correction data requires a GravityState instance (GravityState hold the internal physics configuration of all objects controlled by GE). Since this state will be evolved to simulate the ships path this needs to be a copy of the current GE state retrieved with the GE method GetGravityStateCopy().

The call to ClosestApproach() returns the distance of closest approach. If the result is negative then an error occurred. Either the approach distance was not reached in the specified time (-1) or the real-time limit was exceeded (-2).

Lunar Course Correction Code

A course correction makes use of the ClosestApproach described above three times, with corrections of (0.001, 0, -0.001) applied to the velocity of the spaceship. This provides three approach distances. These are then used to determine the correction required for the specified closest approach and a new simulation is done with that value to determine the resulting approach.

An example is found in the GEConsole command in the OrbitMGController class.

    /// <summary>
    /// Determine the correction required to establish the desired distance to the moon (i.e. that which
    /// was predicted by the preview)
    /// </summary>
    /// <param name="moonName"></param>
    /// <returns></returns>
    public string LunarCourseCorrection(string moonName) {
        NBody moon = GetTargetByName(moonName);
        OrbitData moonOrbit = new OrbitData();
        NBody moonNbody = GetTargetByName(moonName);
        moonOrbit.SetOrbit(moonNbody, centralMass);
        GravityEngine.Instance().SetEvolve(false);
        lcc = new LunarCourseCorrection(spaceshipCtrl.GetNBody(), moon);
        float approachDistance = 0.1f * moonOrbit.a;
        double targetDistance = predictedDistance;
        double targetAccuracy = 0; // Does not matter for closest
        string result = lcc.CorrectionCalcAsync(targetDistance, targetAccuracy, approachDistance, 
                    TIME_TO_MOON, CorrectionCalcCompleted);
        // GravityEngine.Instance().SetEvolve(true);
        return result;
    }

    private void CorrectionCalcCompleted(LunarCourseCorrection lcc) {
        // Update the GE Console
        string s = LunarCorrectionApply();
        GEConsole.Instance().AddToHistory(s);
    }

The CorrectionCalcAsync() call takes a series of parameters to specify the desired approach distance as well as a callback method to run once the computation is completed.

The callback routine can then apply the correction velocity to the ship:

 // Get the final correction and apply it
 double[] v = new double[3];
 lcc.GetCorrectionVelocity(ref v);
 GravityEngine.Instance().SetVelocityDouble(spaceshipCtrl.GetNBody(), ref v);

The final approach distance will be more accurate the later in the transfer it is determined. In practice several course corrections during the transfer are used to achieve the optimal outcome.

N-body Physics

and other interesting stuff…

Lunar Transfer/Lunar Course Correction

Patched Conic Transfer

Lunar Course Correction

Patched Conic/Course Prediction Code

Lunar Course Correction Code