“On-Rails” describes orbital evolution that is computed according to exact two-body equations instead of a full N-body gravitational simulation. On-rails evolution is an approximation that assumes there is a single closest body that affects e.g. a spaceship. This allows the position in the orbit at any given time to be determined. If the ship flies to another planet or moon at some point it moves to a new conic (ellipse, parabola or hyperbola) around the new body. The motion always assumes that the motion is completely determined by one mass at a time. There is no accounting for cases where a spaceship is influenced by more than one mass.
Running all of the bodies in a scene “on-rails” has several advantages. Assuming all objects stay in orbit around the same body, the position at any time can be immediately computed. The time can be jumped forward or backward without the need to compute all the intermediate motion. This form of evolution is not sensitive to numerical integration parameters (time step size).
<GIF of jumping movement forward/backward>
There are disadvantages to on-rails operation. The resulting game physics is an approximation which may be non-physical if there cases where more than one body has a strong gravitational effect. Some interesting gravitational behaviors (e.g. Lagrange points) cannot be modeled on-rails. Motion between a planet and a moon can be approximated with on-rails hand-off, but the resulting motion is not as accurate as an N-body simulation.
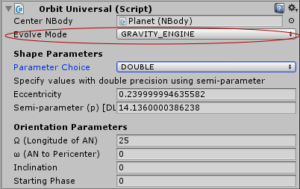
Gravity engine supports full NBody gravitational simulation and on-rails operation as well as combinations of these modes. The orbit classes (e.g. OrbitUniversal) have a mode attribute that can be set to GRAVITY_ENGINE or KEPLER_MODE. KEPLER_MODE is the term used for on-rails operation because Kepler’s equation is used to derive the motion. With each object choosing it’s own evolution, Gravity Engine allows a mix of Kepler and NBody objects and all Kepler (fully “on-rails) operation.
Some game scenarios benefit on other ways from on-rails. Consider the case of ship in a circular orbit around a moon. Depending on the system, there not be a physical/real circular orbit using an NBody gravitational simulation due to the combined effect of the planet and moon on the spaceship (See the LINK inkOrbits-Tutorial scene). By putting the ship “on-rails” around the moon the gravity of the planet is neglected and a circular orbit can be used.
Putting an Object On-Rails (Kepler Mode)
The Orbit classes in Gravity engine can be used in one of two modes:
- Gravity Engine: Use the orbit parameters to define the initial position and velocity and then let N-body evolution proceed from there.
- Kepler Mode (On-Rails) Use the orbit parameters and time to determine the position and velocity at each time update of the gravity engine.
This mode is selected in the inspector for the orbit components. For example for OrbitUniversal:
The video below shows the difference this can have in the case of a ship around a planet in which the planet orbit a star:
<Video Ellipse Moon orbit vs on-rails>
Moving Forward-Backwards in Time (All On Rails)
Gravity Engine checks to see if all objects in a scene are in KEPLER mode orbits or have a FixedObject component. When all objects are on rails there are additional functions that can be used:
public void SetPhysicalTime(double newTime)
This function sets the GE physical (internal) time to the specified value. (If the scene is not all on rails it will issue a warning and ignore the request).
An example of this cane be found in the XXX scene. Here a component TimeSlider has been created to use input from a UI slider on the world canvas to move time forward and backward.
<Video of Time Jump>
ApplyImpulse – Changing On-Rails Motions
NBody objects that are on-rails and use OrbitUniversal can have their orbit modified by the use GravityEngine ApplyImpulse(). This type of orbit allows the evolution of the object to shift between ellipse, parabola and hyperbola as the impulse changes the energy of the orbit. If the object has an OrbitEllipse or OrbitHyperbola an ApplyImpulse will be reported as an error at run-time.
Note that use of ApplyImpulse changes the orbital parameters. If SetPhysicalTime() is used to set a time before the impulse was applied the evolution will not be a true “rewind” since the new orbit parameters will be used at the earlier time. The KeplerSequence component (below) can be used to handle cases where moving time past maneuvers is needed.
On-Rails Orbit Transfers via KeplerSequence
If all that on-rails provided was a fully fixed, clockwork scene, it would have limited use in a space game. The KeplerSequence class allows a sequence of OrbitUniversal elements to be followed with transitions at specific times. For example, to make an orbital transfer there could be a sequence:
- Initial orbit
- Hohmann transfer orbit starting at time t1
- Destination orbit at time t2
With such a sequence in place the time can be jumped to any point and the KeplerSequence will use the appropriate OrbitUniversal for the specified time.
The scene in Scenes/Demos/LambertXferDL-OnRails demonstrates an on-rails transfer and provides a simple slider to manipulate scene time.
<Scene video>
This scene has a spaceship with a KeplerSequence component as well as an OrbitUniversal component. The code in the LambertDemoController has been modified to construct the transfer using either a KeplerSequence when the scene is all on-rails, or using NBody Maneuver classes when the scene is using N-body evolution.
The key code in LambertDemoController is in the TransferOnRails() method. The core code is:
// Kepler sequence already has the initial orbit. // transfer orbit Vector3d xfer_r0 = lambertU.GetTransferPositionDouble(); Vector3d xfer_v0 = lambertU.GetTransferVelocityDouble(); double xfer_t = ge.GetPhysicalTimeDouble(); keplerSeq.AppendElementRVT(xfer_r0, xfer_v0, xfer_t, spaceshipNBody, starNBody, null); // destination orbit double dest_t = xfer_t + transferTime; Vector3d dest_v = new Vector3d(targetData.GetPhysicsVelocityForEllipse(targetData.phase)); Vector3d dest_r = new Vector3d(targetData.GetPhysicsPositionforEllipse(targetData.phase)); keplerSeq.AppendElementRVT(dest_r, dest_v, dest_t, spaceshipNBody, starNBody, SequenceDoneCallback);
The code uses AppendElementRVT to add a new orbit specified by position, velocity and time to the KeplerSequence. Orbits can also be added by providing orbital elements in the form of an OrbitData class.
The KeplerSequence can add new orbit segments in several forms. The API is:
public OrbitUniversal AppendElementRVT(Vector3d r0,
Vector3d v0,
double time,
NBody body,
NBody centerBody,
ElementStarted callback)
public OrbitUniversal AppendElementOrbitData(double time,
OrbitData orbitData,
NBody body,
NBody centerBody,
ElementStarted callback);
public void AppendElementExistingOrbitU(OrbitUniversal orbitU,
ElementStarted callback);
The ElementStarted callback is invoked when the sequence first advances to the new element as part of time evolution.
On-Rails Transfers Between Bodies
The FreeReturnOnRails mini-game demonstrates how on-rails mode can be used with a transfer from a planet to a moon. The current form of this scene is not a full on-rails implementation. Time cannot be arbitrarily jumped forward or backward due to the need to detect the point at which control passes from the planet to the moon.
The scene consists of the following components:
- A spaceship in Kepler mode with an OrbitUniversal (this is key, since when passing the moon, the orbit needs to be a hyperbola).
- A FreeReturnController. This is the same as used for the N-body scene. The code can be common since setting the departure velocity and location is the same in both cases.
- A PatchedConicSOI component (on the same game object as the FreeReturnController). This script monitor the spaceship position and triggers a callback that implements IPatchedConicChange (in this scene this is a OrbitUniversalSOIChange component attached to the spaceship).
- An OrbitUniversalSOIChange component that call OrbitUniversal SetNewCenter() when the dominant source of gravity is changed. This method adjust the current position and velocity to the new center and evolves the orbit using Kepler’s equation with respect to the new center.
The use of a PatchedConicSOI to handle the change of the central body requires that time be evolving forward linearly to ensure that it triggers as the SOI is crossed.