I have developed an enthusiasm (aka weird obsession) for celestial mechanics and developed several games and the Unity Asset Gravity Engine . In developing Gravity Engine I learned a great deal about high pedigree N-body simulations, but in some cases (e.g. a model of the solar system) it is not really necessary to simulate the system but rather just evolve it in the correct way. In this case Gravity Engine offers the option to use Kepler’s equation and move bodies in their elliptical orbit as a function of time. This uses far less CPU than doing the 9*8 mutual gravitational interactions (10*9, if you add in the “dwarf planet” Pluto).
[If you don’t see an animation, click the post title to see ONLY this post. There is WordPress JS bug when this animation and a YouTube link are present]
Creating code to move a planet in an elliptical orbit with the correct velocity is surprisingly tricky. This is one of those cases where you might expect you could just grab a formula from Wikipedia and bang out some code. This bias comes from all the examples in physics class where the goal is to “find/derive the formula” and get a tidy equation.
If you dig around on physics pages for an equation of an elliptical orbit you will generally encounter the equation for the shape of the orbit with eccentricity e, and semi-major axis, a:
I have attached the subscript F to the angle to indicate this is the angle from the focus of the ellipse between the position of the body and the long axis of the ellipse. Historically, this angle is named the True Anomaly.
Where is time in this equation?
Nowhere. This equation doesn’t tell us anything about time.
To get an equation for how the object moves as a function of time, we’ll need Kepler’s equation. Kepler constructed his equation without Calculus (which came along about 60 years after Kepler did this work) using geometric arguments and the assumption that an objects speed in an elliptical orbit was inversely proportional to it’s distance from the focus. Kepler’s equation is:
Here M is the position of a body moving in a uniform circle at a constant rate (that we will relate to time) and E is the angle to the position on the ellipse from the origin, called the eccentric anomaly. Here a picture will help:
The eccentric anomaly is NOT the same angle as
(f in the picture) however they can be related with a bit of geometry:
.
If we have a specific time we want a position for we need to convert this into a value of M. This is done by dividing the time by the time per orbit, T. Kepler can also help us here with his third law that relates the size and eccentricity of the orbit to the mass of the bodies:
where m is the combined mass of the central object and orbiting body. (Kepler did not know the proportionality constant was the mass, that came later).
Given M, Solve for E
Ok, we’ll just isolate E…hmmm. E appears by itself and inside the sine function. That sinks our chance of getting a tidy mathematical formula. This equation is legendary in Mathematics, since it is an early example of a transcendental equation with an import application. It has been studied extensively and the approaches are well summarized in the book “Solving Kepler’s Equation Over Three Centuries” by Peter Colwell.
There are some series approximations, but they are not valid for all eccentricities. The most common approach is to iterate the equation until we converge on a value that is “good enough”.
The “recipe” for tying this all together is:
- Determine the orbital period T
- For the time t we’re interested in, divide by the orbital period and use the remainder to find the angle if the body were moving in a uniform circle, M.
- Using iteration solve Kepler’s equation and find E
- Using E, determine
- Find the corresponding r using the orbit equation.
In Javascript this becomes:
var orbitPeriod = 2.0 * Math.PI * Math.sqrt(a*a*a/(m*m)); // G=1
function orbitBody() {
// hide last position drawn
context.clearRect( last_x -10, last_y - 10, 20, 20);
// 1) find the relative time in the orbit and convert to Radians
var M = 2.0 * Math.PI * time/orbitPeriod;
// 2) Seed with mean anomaly and solve Kepler's eqn for E
var u = M; // seed with mean anomoly
var u_next = 0;
var loopCount = 0;
// iterate until within 10-6
while(loopCount++ < LOOP_LIMIT) {
// this should always converge in a small number of iterations - but be paranoid
u_next = u + (M - (u - e * Math.sin(u)))/(1 - e * Math.cos(u));
if (Math.abs(u_next - u) < 1E-6)
break;
u = u_next;
}
// 2) eccentric anomoly is angle from center of ellipse, not focus (where centerObject is). Convert
// to true anomoly, f - the angle measured from the focus. (see Fig 3.2 in Gravity)
var cos_f = (Math.cos(u) - e)/(1 - e * Math.cos(u));
var sin_f = (Math.sqrt(1 - e*e) * Math.sin (u))/(1 - e * Math.cos(u));
var r = a * (1 - e*e)/(1 + e * cos_f);
time = time + 1;
// animate
last_x = focus_x + r*cos_f;
last_y = focus_y + r*sin_f;
drawBody( r* cos_f, r*sin_f, "blue");
setTimeout(orbitBody, 30);
}
I have left out some of the init code for clarity. If you view the source for this page you can find all this.
(Eccentric anomaly image created by CheCheDaWaff/Creative Commons License).

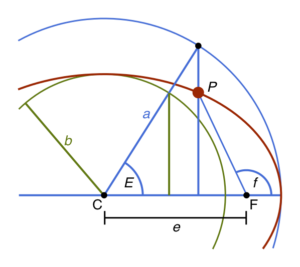
Thanks nbody, that algorithm was exactly what I was struggling to find for adding precession to my Universal Community Calendar application. I understood just enough of it to get it working. The app is at http://tomboy-pink.co.uk/codelib/UCC/calclock.html, if you’re interested.
FYI, the Asset Store link always to be broken after the many changes they’ve made to the Asset Store website.
This appears to be a good link: https://assetstore.unity.com/packages/tools/game-toolkits/gravity-engine-62432
Thanks! Fixed.