The thing I love about having diverse customers for Gravity Engine is that the questions they raise force me to extend my knowledge of orbital mechanics beyond the “simple” treatments presented in the textbooks. Recently, the developer of the very impressive ReEntry game highlighted the fact that the Hohmann and Lambert rendezvous code in Gravity Engine was cool, but it did not match the method used by NASA for Gemini and Apollo rendezvous. NASA used a maneuver called trigger angle targeting that used a burn in the line of sight direction from the ship to the target. Ok, I thought, time to dig through my 12 orbital mechanics books and see what’s up with this. Only two of the books mentioned this mode of rendezvous. Walter’s Astrodynamics mentions this in an informational box on NASA rendezvous techniques and provides some references. Practical Astrodynamics by de laco Veris presents an iterative solution.

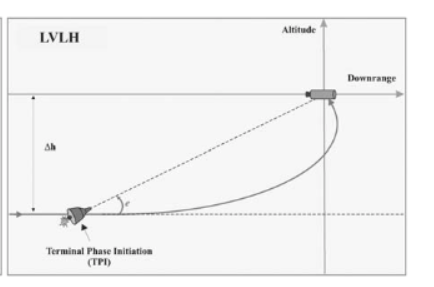
First a bit of background on this technique in the context of Apollo lunar rendezvous. This rendezvous mode is used in the final phase of rendezvous when the LM and CM are already in circular coplanar orbits with a modest difference in radius (e.g. 28 km). The LM catches up from below and behind and when the CSM is at a specific angle above the horizon (about 27 degrees) it burns directly towards the CSM. This has the advantage of allowing a manual orientation and burn in the event of computer issues or loss of communication. Point the ship at the target and burn. The burn magnitude is based on a calculation that factors in the desired time to rendezvous. In the Apollo case the time to rendezvous was chosen such that the CSM moved through about 130 degrees of it’s orbit.

I first considered the usual rendezvous approaches to see how they compared. A Hohmann transfer requires the CSM to move through 180 degrees and has a burn direction parallel to the local horizon. It is the most efficient transfer but the ship needs to be pointed towards the horizon. A Lambert transfer to the desired rendezvous point could be done but the velocity vector is unconstrained and in general will not be in the direction of the CSM. Quantitatively how do these compare to the actual Apollo 11 burn?

Type	Angle from Horizon (deg)	Burn Magnitude (m/s)
Hohmann	0	6.62
Lambert	20.97	7.83
Trigger Angle	25.54	8.24

Note that the trigger angle is a more expensive option in terms of dV. The fault tolerant procedure comes at a cost. Neither the Hohmann or Lambert transfer is providing the trigger angle burn needed for Apollo 11. Gravity Engine clearly needs some new code.

The trail starts with a paper from 2007 by Woffinden, Rose and Geller that demonstrates how to solve for a trigger angle given that the burn must be in the direction of the target. I found it a bit surprising that this analytic result was published 45 years after trigger angle targeting was used in Gemini! This paper also references the very readable Navigating the Road to Autonomous Orbit Rendezvous by Woffinden and Geller.

The approach taken in the trigger angle paper is to use a local co-rotating co-ordinate system with the rendezvous target at the origin. This system assumes the target is in a circular orbit and the ship is “relatively close” to the target. This system is often referred to an Local Vertical Local Horizontal or LVLH. The rendezvous equations can be mapped into this co-ordinate system with a few simplifying assumptions and the result is the Hill-Clohessy-Wiltshire equations that describe the relative motion of the ship with respect to the fixed target.

The new code added to Gravity Engine provides a RelativeMotion class that provides the Hill-Clohessy-Wiltshire rendezvous equations and an additional module to perform the trigger angle targeting. The result of this code for the Apollo 11 case produces the trigger angle and burn shown in the table above. When used “as is” the resulting rendezvous in the fixed target frame is:

By itself this burn does not result in a perfect rendezvous. After braking the LM is 3.55 km away from the CSM with a residual velocity of 2.9 m/s. Further nuance is needed.

The Apollo 11 terminal phase included two course correction burns and a series of braking maneuvers at fixed distances from the CSM (LM burn schedule). To include this a TPIBurn class has been added to Gravity Engine to handle the sequencing of these events in addition to the initial TPI burn. By adding these elements to the scene the rendezvous now concludes with the LM 21 meters away from the CSM with a negligible residual velocity.

This code will be available in Gravity Engine release 5.0.